[Paper Review] LoRA: Low-Rank Adaptation of Large Language Models
지난 포스트에서 살펴봤듯이, GPT-3는 모델 크기 확장과 in-context learning으로 Zero-shot 성능을 크게 끌어올렸습니다. 하지만 여전히 fine-tuning이 필요한 영역은 존재합니다. GPT-3 저자들은 아래와 같이 모델의 한계를 확인했는데요. 저자들이 추정한 원인은 단방향 LM이 지닌 구조적 문제와 fine-tuning의 부재였습니다.
| Task | GPT-3 175B few-shot 성능 | 기존 Fine-Tuned SOTA | 한계점 |
|---|---|---|---|
| Natural Language Inference | - ANLI R3 $\approx$ 40% - RTE 69% - WiC 49% (동전 던지기 수준) | - ANLI R3 48% - RTE 93% - WiC 76.1% | 비교·함의 과제에서 낮은 성능 |
| 독해·다중 단서 통합 | - RACE-h 47% - QuAC 44 F1 - DROP 37 F1 | - RACE-h 90% - QuAC 74 F1 - DROP 89 F1 | 장문 이해·수치 추론에서 큰 격차 |
| 과학·상식 QA | - ARC-C 51% - OpenBookQA 65% | - ARC-C 78% - OpenBookQA 87% | 배경지식+추론 결합 문제에 취약 |
| 번역 | - En→Ro 21 BLEU - En→De 29 BLEU | - En→Ro 38 BLEU - En→De 41 BLEU | 영어 편중 데이터·BPE 한계 |
| 4-5 자리 산수 | 10~30% | - | 토큰 단위 예측은 체계적 알고리즘 수행 어려움 |
이렇듯 고난이도의 task를 fine-tuning 없이 해결하는 것은 아직 한계가 있습니다. 하지만 Language Model의 크기가 점점 커지는데, full fine-tuning은 현실적으로 불가능합니다. 이러한 상황에서 LLM을 효율적으로 fine-tuning하기 위해 제안된 모델이 바로 LoRA(2021)입니다. 기존 weight는 그대로 두고, 저차원 보조 행렬만 학습해 메모리를 크게 줄이면서도 전체 fine-tuning과 동등한 성능을 달성했습니다.
1. 등장 배경
pre-trained autoregressive language model $P_{\Phi}(y \mid x)$를 full fine-tuning 하는 과정을 생각해보겠습니다. 다음과 같은 목적함수를 최대화하는 과정에서 $\Phi_0$로 초기화되었던 모델 weight가 $\Phi_0 + \Delta \Phi$로 업데이트되고, 이를 계속해서 반복합니다. \(\max_{\Phi} \; \sum_{(x, y) \in \mathcal{Z}} \; \sum_{t=1}^{|y|} \log \left( P_{\Phi}(y_t \mid x, y_{<t}) \right )\) 이러한 full fine-tuning 방식의 단점은 각각의 downstream task마다 서로 다른 파라미터 $\Delta \Phi$를 학습해야 한다는 것입니다. GPT-3의 경우에는 학습해야 하는 파라미터 수 $| \Delta \Phi | = | \Phi_0 |$가 최대 175B에 달합니다.
저자들의 주장에 따르면, LLM이 학습하는 정보는 몇 가지 중요한 패턴들 만으로도 표현 가능합니다. 다시 말해, 모델이 아무리 커도 핵심적인 정보는 그 안의 작은 subspace에 들어있다는 것입니다. 그렇기 때문에 매번 파라미터 전체 $\Delta \Phi$를 업데이트할 필요는 없고, 그보다 훨씬 적은 수의 파라미터 $\Theta$만 학습하면 된다는 것이 저자들의 주장입니다. $\Delta \Phi$를 $\Theta$의 함수 $\Delta \Phi(\Theta)$로 두고, $\Theta$를 학습하도록 바꾸면 목적함수는 아래와 같습니다. \(\max_{\Theta} \; \sum_{(x, y) \in \mathcal{Z}} \; \sum_{t=1}^{|y|} \log \left( p_{\Phi_0 + \Delta \Phi(\Theta)} \bigl( y_t \mid x, y_{<t} \bigr ) \right )\)
2. 모델 구조
Rank
LoRA의 모델 구조에 대해 알아보기 전에, rank에 대해 간단히 설명하고 넘어가겠습니다. rank는 행렬이 표현할 수 있는 독립적인 vector의 개수를 말합니다.
\[M = \begin{bmatrix}2&4\\1&2\\ \end{bmatrix}\]예를 들어 위 행렬의 rank는 1입니다. 첫 번째 vector에 2를 곱하면 두 번째 vector를 얻을 수 있기 때문입니다.
\[M = \begin{bmatrix}1&0\\0&1\\ \end{bmatrix}\]위 행렬에서는 한 vector가 다른 vector의 배수로 표현되지 않습니다. 다시 말해 두 vector는 선형 독립이고, rank는 2입니다. 위에서 설명했던 몇 가지 중요한 패턴들이란 이러한 vector들을 말합니다.
학습 및 추론 과정
모델의 학습 및 추론 과정을 정리해보면 아래와 같습니다.
- rank $r$ 선택 – 보통 4~16
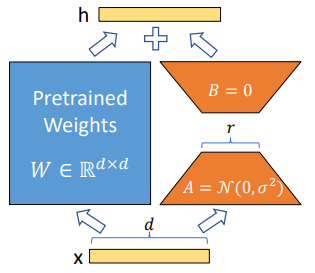
- 각 Transformer weight $W$ ($d \times d$) 옆에 $A$ ($r \times d$), $B$ ($d \times r$) 두 행렬을 삽입
- 학습 중엔 $A$, $B$만 업데이트 → 연산량 증가 $\le$ 1%
- 추론 시엔 $W + A \cdot B$를 미리 합쳐 두어 추가 지연 발생하지 않음
일반적인 fine-tuning에서는 $d \times d$ 크기의 $\Delta W$을 학습합니다.
\[h=W_0x+\Delta Wx\]하지만 LoRA는 $\Delta W$를 $B \cdot A$로 표현하여 $d \times r + r \times d$개의 파라미터만을 학습합니다.
\[h=W_0x+\Delta Wx = W_0x+B(Ax)\]여기에서 $A$는 $x$를 $r$-차원으로 줄이는($Ax$) 역할을, $B$는 그 값을 다시 $d$-차원 공간으로 펼치는 역할을 합니다. 결과적으로 $\Delta W$는 rank가 $r$ 이하인 행렬이 되어 저차원의 변화량만을 학습할 수 있게 되는 것입니다.
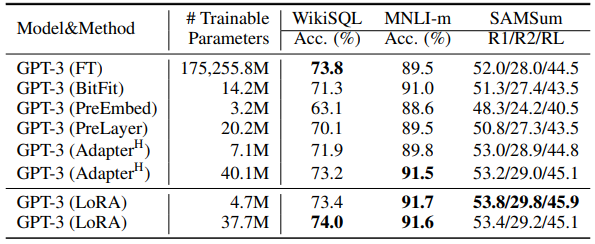
3. 모델 성능
위 성능 결과 표에서도 확인할 수 있듯이, LoRA는 매우 적은 수의 파라미터(4.7M)만을 학습해서 GPT-3 full fine-tuning(FT)과 비슷하거나 더 좋은 성능을 달성했습니다. 학습 파라미터 수는 약 37,000배 감소시켰습니다.