Generative Adversarial Networks

딥러닝 기반 생성 모델이 등장하기 전에는 주로 Markov chain과 같은 통계적인 방법에 의존해 데이터의 분포를 모델링하고, sample을 생성했습니다. 이 모델들은 이미지와 텍스트같이 복잡한 분포를 가진 데이터들을 모델링하는데 한계가 있었는데요. VAE, GAN과 같은 딥러닝 기반 생성 모델들은 neural network로 구성되어 있어 backpropagation으로 학습할 수 있고, 데이터를 보다 풍부하게 표현할 수 있습니다.

본 포스트에서는 GAN부터 WGAN-GP까지 GAN 계열 모델의 발전 과정을 훑어보면서 각 모델의 한계점과 이전 모델보다 나아진 점들을 짚어보려고 합니다. GAN을 소개하기에 앞서 GAN과 같은 딥러닝 기반 생성 모델의 일종인 VAE와 GAN의 차이점에 대해 알아보겠습니다.

1. GAN과 VAE 비교

1-1. 모델링 대상

• VAE는 explicit distribution을 모델링
  • VAE는 입력 데이터의 잠재 공간 $z$에 대한 사전 확률 분포 $p(z)$를 명시적으로 설정하고, 입력 $x$에 대해 사후 분포 $q(z \vert x)$를 학습
  • encoder는 입력 데이터를 기반으로 잠재 공간에서의 평균(mean)과 분산(variance)을 출력하고, 이 평균과 분산을 사용해 잠재 공간에서 샘플링을 수행하여 새로운 데이터를 생성
• GAN은 implicit distribution을 모델링 (VAE 보다 좀 더 practical)
  • GAN에서 생성기는 임의의 noise 벡터를 받아 실제 데이터와 유사한 데이터를 생성하는 함수를 학습
  • 판별기는 실제 데이터와 생성된 데이터를 구분하는 기능을 학습
  • 생성기의 목적은 판별기를 속이는 것이므로, 생성기는 결국 실제 데이터 분포를 모방하는 데이터를 생성할 수 있는 함수를 간접적으로 학습하게 됨

1-2. 분포 사이의 유사성을 측정하는 metric

• VAE는 KL divergence 사용
  • 두 분포 $p$와 $q$가 주어졌을 때, $p$가 $q$에 대해 얼마나 다른지 측정
  • KL divergence는 비대칭(asymmetric)
• (Vanila) GAN은 JS divergence 사용
  • 두 분포 $p$과 $q$가 주어졌을 때, 두 분포의 중간 지점과의 차이를 측정
  • JS divergence 는 대칭(symmetric)

2. GAN (2014)

GAN architecture

모델 구조 및 학습 과정

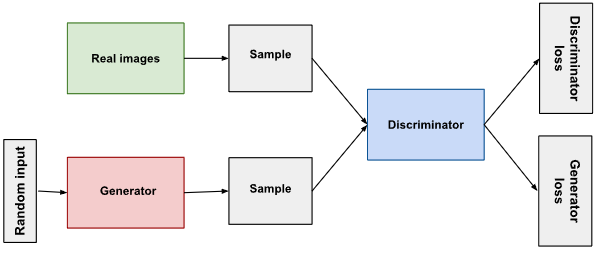
GAN은 위 그림과 같이 생성기(Generator)와 판별기(Discriminator)로 구성되어 있습니다. 생성기의 역할은 판별기가 구분하기 어려운, 진짜같은 이미지를 생성하는 것입니다. 판별기의 역할은 주어진 sample이 생성기가 생성한 가짜인지 진짜 학습 데이터인지 판별하는 것입니다. 판별기는 0과 1 사이의 확률값을 출력하는데, 1에 가까울수록 주어진 sample이 진짜 이미지에 가깝다는 것을 의미합니다. 생성기와 판별기의 상호작용은 아래와 같은 minimax 게임으로 표현됩니다.

\[\underset{G}{\min}\,\underset{D}{\max}\,V(D, G)=E_{x \sim p_{data}(x)}[logD(x)]+E_{z \sim p_{z}(z)}[log(1-D(G(z)))]\]

판별기 학습 시에는 생성기를 고정시키고, 반대로 생성기 학습 시에는 판별기를 고정시킵니다.

\[\underset{D}{\max}\,V(D, G)=E_{x \sim p_{data}(x)}[logD(x)]+E_{z \sim p_{z}(z)}[log(1-D(G(z)))]\] \[\underset{G}{\min}\,V(D, G)=E_{z \sim p_{z}(z)}[log(1-D(G(z)))]\]

위 과정을 반복하면서 생성기와 판별기가 서로 경쟁하면서 학습합니다. 최종적으로는, 생성기가 만든 이미지가 진짜인지 가짜인지 판별기가 구분할 수 없어서($p_{data}=p_g$) 판별기의 output이 0.5에 가까워지는 것이 목표인데요. 이 과정을 좀 더 자세히 설명해보면 다음과 같습니다.

GAN 학습 과정

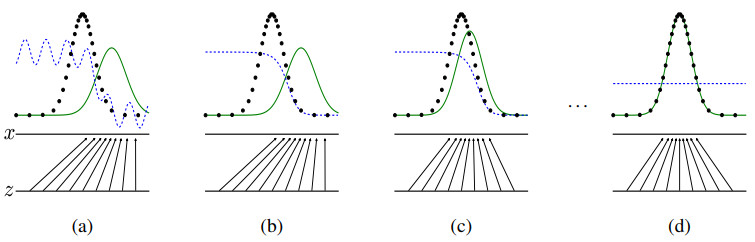
검정 점선은 실제 분포 $p_{data}$, 초록 실선은 가짜 분포 $p_{g}$, 파란 점선은 판별기의 분류 결과를 나타냅니다. (a) 학습 초기에는 판별기가 충분한 학습을 하지 못해서 주어진 이미지의 진위 여부를 불안정하게 예측합니다. 어느 정도 학습이 진행되면, (b) 판별기가 실제 데이터와 가짜 데이터를 잘 분류할 수 있게 되고, (c) 생성기도 학습 초기보다는 실제 데이터와 유사한 이미지를 생성합니다. (b)와 (c)가 반복되며 학습이 진행되다가 (d) 최종적으로 가짜 이미지의 분포가 실제 이미지의 분포와 동일해지면($p_{g}=p_{data}$) 판별기가 두 분포를 구분하지 못하고, 모든 데이터 포인트 $x$에서 0.5를 출력하게 됩니다($D(x)=0.5$).

실험 결과

저자들이 GAN 학습에 사용한 데이터셋은 MNIST, TFD(Toronto Face Database)와 CIFAR-10 입니다. 실험 시 생성기에는 ReLU와 Sigmoid를 사용했고, 판별기에는 maxout과 Dropout을 사용했습니다. 저자들이 실험 결과를 통해 주장하는 GAN의 장점은 다음과 같습니다.

• 생성기는 학습 데이터를 통해 직접 업데이트되는 것이 아니라, 판별기로부터 전달된 gradient를 통해 업데이트 됩니다. 따라서 생성기가 생성하는 이미지는 학습 데이터를 단순히 암기한 것이 아닙니다.

• Markov chains 기반 모델들과 비교했을 때, 흐릿하지 않고 또렷한 이미지를 생성할 수 있습니다.

  

  

• latent vector 사이의 interpolation으로도 있을 법한 이미지를 생성할 수 있습니다.

3. Deep Convolutional GAN (2015)

DCGAN generator architecture

모델 구조

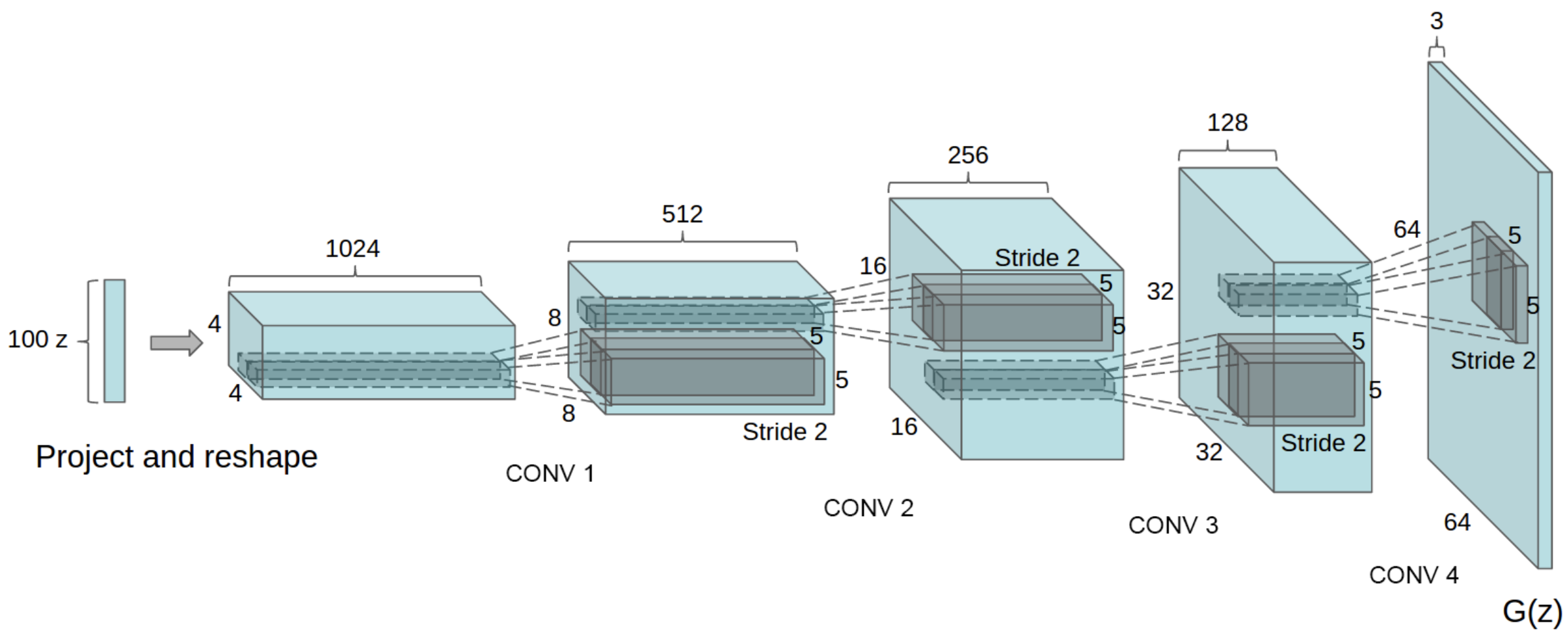
앞서 설명한 GAN은 생성기와 판별기 학습할 때 MLP 구조를 사용했는데, DCGAN은 CNN 구조를 사용합니다. 이러한 차이로 GAN보다 고해상도의 이미지를 생성할 수 있습니다. DCGAN도 GAN과 마찬가지로 생성기와 판별기로 구성됩니다. 생성기와 판별기가 각각의 output을 출력하는 과정은 다음과 같습니다.

• 생성기
  • Step 1 표준 정규분포로부터 랜덤 샘플링된 100 차원의 vector $z$를 입력받음
  • Step 2 fully connected layer를 통과시켜서 $4 \times 4 \times 1024$ 차원의 vector를 생성
  • Step 3 activation map 형태(height 4, width 4, channel 1024)로 Reshape
  • Step 4 transposed convolution를 사용해 너비와 높이를 증가시킴 (upsampling)
  • Step 5 최종적으로 RGB 형태(height 64, width 64, channel 3)의 output 출력
  • activation function
    • 출력 layer에는 Tanh, 그 외에는 ReLU 사용
    • -1과 1사이의 출력 layer output을 0과 255 사이의 값으로 변환
• 판별기
  • Step 1 생성기의 output(가짜 이미지)과 실제 이미지를 입력받음
  • Step 2 strided convolution를 사용해 너비와 높이를 감소시킴 (downsampling)
  • Step 3 최종적으로 주어진 sample이 진짜(1)인지 가짜(0)인지 출력
  • activation function
    • 출력 layer에서는 Sigmoid, 그 외에는 Leaky ReLU 사용
    • 출력 layer의 최종 output은 Real(1), Fake(0)

실험 결과

저자들이 DCGAN 학습에 사용한 데이터셋은 아래와 같습니다.

• LSUN (Large-scale Scene Understanding) Dataset: 특히 LSUN 데이터셋의 ‘bedrooms’ 카테고리가 사용되었습니다. 이 데이터셋은 약 300만 개의 이미지를 포함하고 있으며, 주로 방의 이미지로 구성되어 있습니다.
• Imagenet-1K: 32x32 크기로 center crop한 이미지를 사용했습니다.
• Faces Dataset: 인터넷에서 무작위로 수집한 사람들의 이름을 기반으로 한 35만 개의 얼굴 이미지로 구성되어 있습니다.

• 임의의 두 vector $z_1$, $z_2$를 interpolation한 vector들을 생성기에 입력해 결과 이미지를 나열했을 때, 부드러운 transition이 나타나는 것을 확인할 수 있습니다.

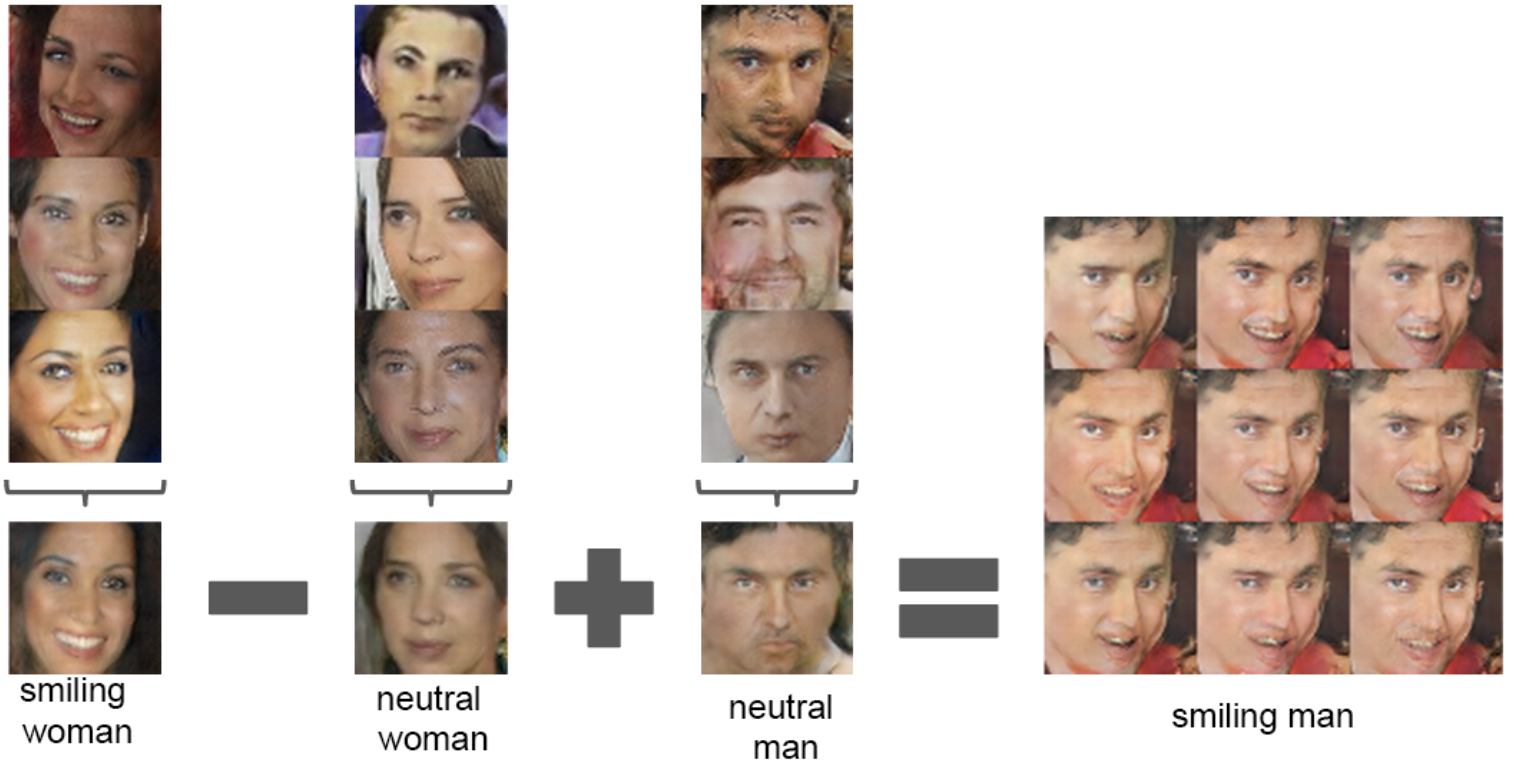
• 위 결과는 DCGAN이 얼굴에서 나타나는 다양한 특성을 적절하게 인코딩했음을 보여줍니다. 웃는 여성 이미지를 만드는 vector들의 평균 값(smiling woman)에서 무표정한 여성 이미지를 만드는 vector들의 평균 값(neutral woman)을 빼면, 여성이라는 특성은 지워지고 웃는다는 특성만 남습니다. 여기에 무표정한 남성 이미지를 만드는 vector들의 평균 값(neutral man)을 더해 생성기에 입력하면 웃는 남성 이미지가 생성됩니다.

4. Mode collapse

Mode collapse는 GAN을 학습할 때 발생하는 주요 문제들 중 하나입니다. 이 문제는 생성자가 판별자보다 뛰어난 경우에 발생하는데요. 판별자의 성능이 좋지 않을 때, 생성기가 판별기를 쉽게 속일 수 있는 몇 개의 이미지를 찾아낸 다음에는 그 이상 다양한 이미지를 생성할 수 없게 되는 상태를 말합니다. 판별기가 구분할 수 없는 이미지를 생성하는 것이 생성기의 목적인데, 이 목적을 달성했으니 더이상 학습할 동기가 없어지는 것입니다. 또한 이 경우에는 loss function의 gradient가 0에 가까운 값이 되므로 이 상태에서 벗어날 수 없게 됩니다. 이 문제를 해결하기 위해 강력한 판별자를 학습시키는 다양한 모델들이 제안되었는데요. 본 포스트에서는 Unrolled GAN, WGAN과 WGAN-GP를 다뤄보겠습니다.

4-1. Unrolled GAN (2017)

• optimal point $\theta^\ast={ \theta_G^\ast, \theta_D^\ast }$에 도달하기 어려운 이유

  • GAN의 학습 과정은 결국 $\theta_D^\ast$에 의해 최대화된 함수 $f$를 최소화하는 $\theta_G^\ast$를 찾는 과정

    \[\theta_G^\ast=\arg\underset{\theta_G}{\min}\underset{\theta_D}{\max}f(\theta_G, \theta_D)=\arg\underset{\theta_G}{\min}f(\theta_G, \theta_D^\ast(\theta_G))\]

  • 다시 말해, $\theta_D^\ast$를 찾아야 $\theta_G^\ast$를 찾을 수 있는데 $\theta_D^\ast$는 고정된 것이 아니라 $\theta_G$에 따라 변함

    \[\theta_D^\ast(\theta_G) = \arg\underset{\theta_D}{\max}f(\theta_G, \theta_D)\]

  • 많은 시간과 자원을 들여서 $\theta_D^\ast$를 찾았다고 하더라도, 이는 $\theta_G$로 찾은 것이지 $\theta_G^\ast$로 찾은 것이 아님

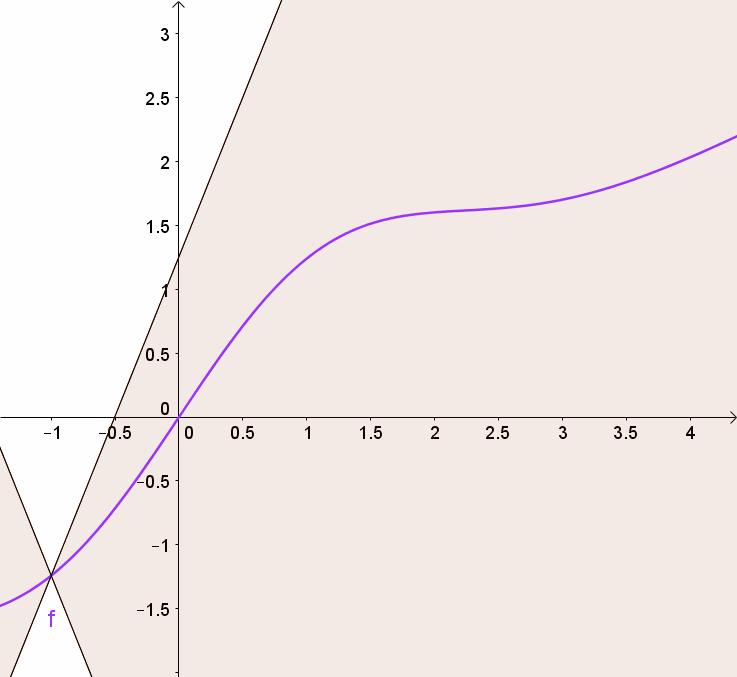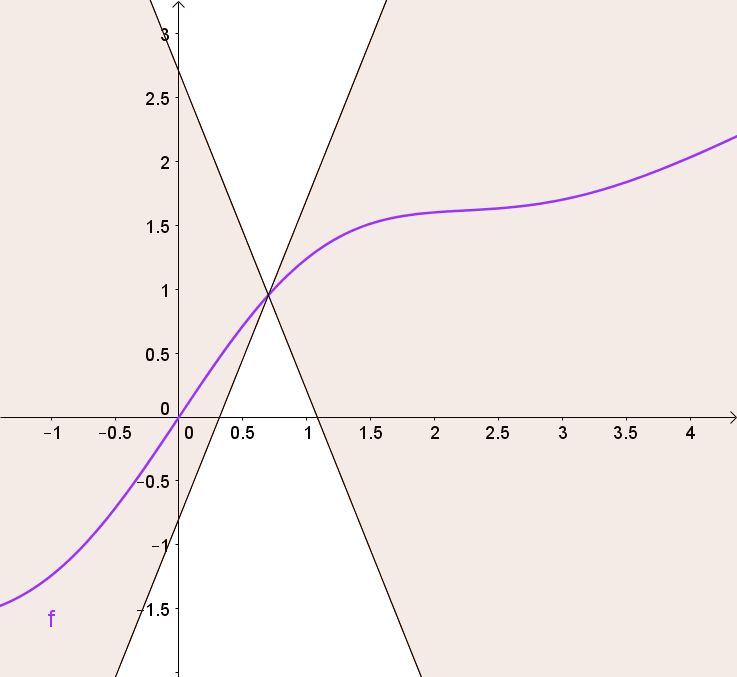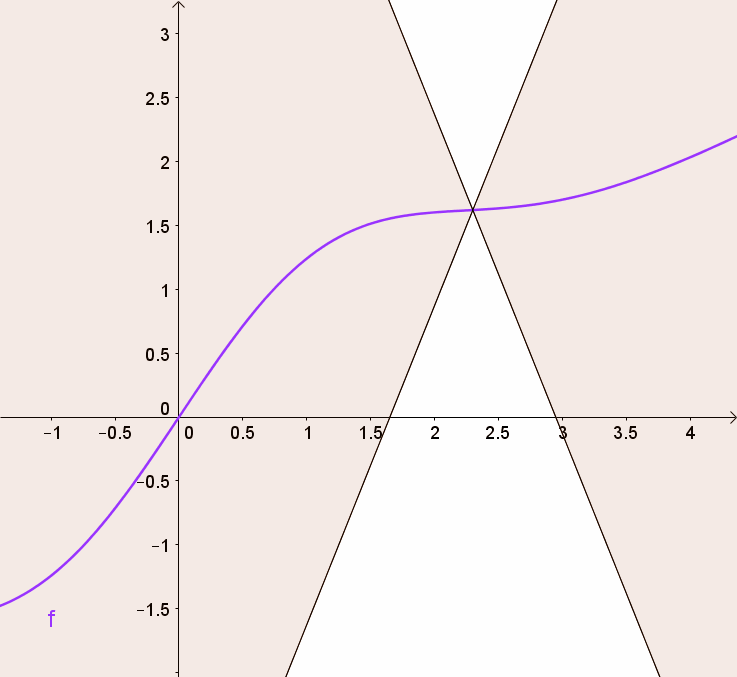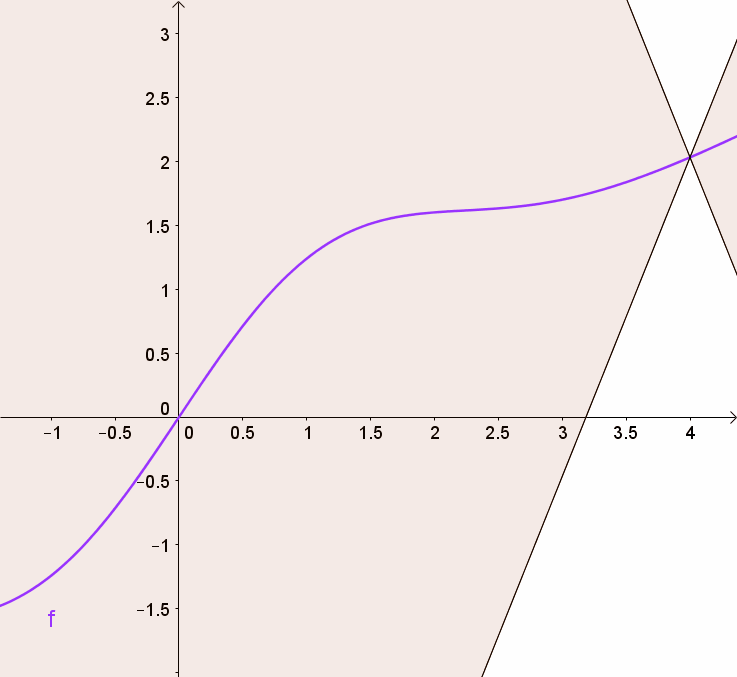
    \[\theta_D^\ast(\theta_G) \ne \theta_D^\ast(\theta_G^\ast)\]

  • $f(\theta_G, \theta_D)$는 단순 convex, concave 함수가 아닐 확률이 높고, 이 경우 greedy한 gradient method를 사용하면 local optimum에 빠지기 쉬움

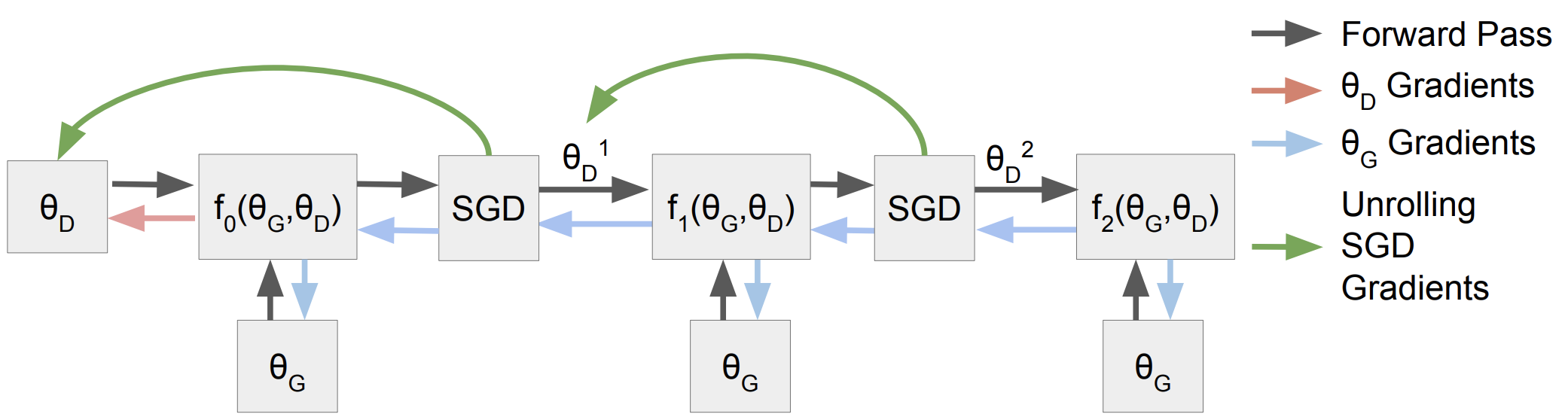
• $\theta_D^\ast$ 대신에 $\theta_D^k$를 사용하는 것이 unrolled gan의 핵심

  • 현실적으로 최적의 판별기 $\theta_D^\ast$를 구하는 것은 어려우므로, 판별기를 k번 업데이트한 $\theta_D^k$를 사용하는 것

    \[f(\theta_G, \theta_D^\ast(\theta_G)):f_K(\theta_G,\theta_D)=f(\theta_G, \theta_D^K(\theta_G, \theta_D))\]

  • 생성기와 판별기를 한 번씩 순서대로 업데이트 하는 것이 아니라, 판별기를 $k$번 업데이트($\theta_D^k$)하고 생성기를 업데이트한 다음, 다시 판별기를 $k$번 업데이트 하고 생성기를 업데이트하는 과정을 반복.

    \[\theta_D^{k+1}=\theta_D^k+\eta^k\frac{df(\theta_G, \theta_D^k)}{d\theta_D^k}\]

  • $k$가 무한대로 가면, 이론적으로는 $\theta_D^\infty \rightarrow \theta_D^\ast$

    \[\theta_D^\ast(\theta_G)=\underset{k \rightarrow \infty}{\lim}\theta_D^k\]

4-2. Wasserstein GAN (2017)

• GAN의 고질적인 문제인 Mode collapse와 불안정한 학습 문제를 해결하기 위해, loss fucntions으로 JS divergence 대신 Wasserstein distance(Earth-Mover distance)를 사용
  • $y$ 값으로 0과 1이 아니라 -1과 1을 사용
  • 판별기의 출력 layer에서 Sigmoid를 제거하여 output이 $[0, 1]$ 범위로 제한되지 않고, $[-\infty, \infty]$ 범위의 어떤 값이든 될 수 있음
• GAN의 loss function을 Wasserstein distance formula로 바꾸는 방법
  • Wasserstein distance는 $\gamma$를 잘 선택해서 이동 비용을 최소화하는 최적화 문제
  • Wasserstein distance의 primal form이 아니라 dual form을 활용할 수 있음
  • Kantorovich-Rubinstein Theorem

\[\begin{align*} W_1(p_{data},p_g) &= \inf_{\gamma \in \Pi(p_{data},p_g)} \mathbb{E}_{(x,y)\sim\gamma}[\|x - y\|] \\ &= \sup_{\vert\vert f \vert\vert_L \leq 1} [E_{x \sim p_r}[f(x)]-E_{y \sim p_g}[f(x)]] \end{align*}\]

• weight를 $[-0.01, 0.01]$ 범위로 제한하는 weight clipping 방법을 사용해 1-Lipshichtz 조건 $\vert\vert f \vert\vert_L \leq1$을 만족하도록 함으로써 안정적인 학습을 유도

  • Lipshichtz 함수는 임의의 두 지점의 기울기가 어떤 상숫값 이상 증가하지 않는 함수(이 상수가 1일 때 1-Lipshichtz 함수). 거의 모든 점에서 연속적으로 미분 가능

    

  • 임의의 두 입력 이미지 $x_1$와 $x_2$에 대해 다음 부등식을 만족하도록 하는 것
  • $\vert x_1 - x_2 \vert$는 두 이미지 픽셀의 평균적인 절댓값 차이
  • $\vert D(x_1) - D(x_2) \vert$는 판별기 예측 간의 절댓값 차이
  • 즉, 두 이미지 사이에서 판별기의 예측이 변화하는 비율의 절댓값이 어디에서나 최대 1이어야 함

\[\frac{ \vert D(x_1) - D(x_2) \vert }{ \vert x_1 - x_2 \vert } \le 1\]

4-3. WGAN-GP (2017)

• WGAN은 weight clipping을 사용했기 때문에 학습 속도가 너무 느리다는 한계점이 있음
• WGAN-GP는 gradient penalty를 이용하여 WGAN의 성능을 개선

Reference

• From GAN to WGAN
• GAN 구조 개요