[Paper Review] DDPM: Denoising Diffusion Probabilistic Models (2)
이번 포스트에서는 지난 포스트에 이어 Denoising Diffusion Probabilistic Models에 대해 좀 더 자세히 알아보겠습니다. 지난 포스트에서 설명한 바와 같이, DDPM은 데이터에 노이즈를 점진적으로 확산시킨 다음, 그 과정을 거꾸로 학습합니다.
정방향 확산 과정
먼저 정방향 확산 과정에서는 매 step마다 노이즈를 $\beta_t$만큼 주입하면서 전체 분산은 그대로 1로 유지하고자 합니다. 이 조건을 만족시키기 위해 $x_t$를 만드는 과정을 아래와 같이 정의합니다.
\[q(x_t \vert x_{t−1}) = \mathcal{N}(\sqrt{1-\beta_t}x_{t-1},\;\beta_t\mathbf I)\]위 식을 유도하기 위해 이전 step $x_{t-1}$과 가우시안 노이즈 $\varepsilon_t$의 선형 결합으로 $x_t$를 정의해 보겠습니다.
\[x_t=a_t x_{t−1} + b_t \varepsilon_t,\qquad \varepsilon_t \sim \mathcal N(\mathbf 0,\mathbf I)\]위 식에서 $a_t$는 이전 step 정보를 얼마나 축소할 것인지를 의미하고, $b_t$는 이번 step에 노이즈를 얼마나 주입할 것인지를 의미합니다.
조건 1: 노이즈를 $\beta_t$만큼 주입
매 step마다 $\beta_t$만큼의 노이즈를 주입한다는 것은 노이즈의 분산 $\text{Var}(b_t\varepsilon_t)$을 $\beta_t$로 만든다는 의미입니다.
\[\text{Var}(b_t\varepsilon_t)=b_t^2\text{Var}(\varepsilon_t)=b_t^2\qquad(\because \text{Var}(\varepsilon_t)=1)\]$b_t^2=\beta_t$가 되려면 $b_t=\sqrt{\beta_t}$가 됩니다.
조건 2: 전체 분산을 1로 유지
다음으로, 이전 step의 분산 $\text{Var}(x_{t-1})$을 1이라고 가정했을 때 $\text{Var}(x_t)$도 1로 유지하려면 아래 식을 만족해야 합니다.
\[\text{Var}(x_t) = \text{Var}(a_tx_{t-1} + b_t\varepsilon_t) = a_t^2\text{Var}(x_{t−1}) + b_t^2\text{Var}(\varepsilon_t) = a_t^2+b_t^2 = 1\]이 때, $b_t=\sqrt{\beta_t}$이므로, $a_t=\sqrt{1-\beta_t}$가 됩니다.
\[x_t = \sqrt{1-\beta_t}x_{t-1} + \sqrt{\beta_t}\varepsilon_t, \qquad \varepsilon_t \sim \mathcal N(\mathbf 0,\mathbf I)\tag{1}\]다시 말해 $x_t$는 이전 step의 정보 $x_{t-1}$을 $\sqrt{1-\beta_t}$만큼 줄이고, $\sqrt{\beta_t}$만큼의 가우시안 노이즈를 더한 것입니다. 이 과정을 여러 번 반복하면 이전 step의 정보 $x_{t-1}$는 계속 줄어들고 가우시안 노이즈가 누적됩니다. 결과적으로, 초기 분산이 1로 정규화된 경우에 충분히 큰 $T$에서는 원본 정보가 거의 0에 수렴하고 분산은 1로 유지됩니다. $x_T$가 표준 정규 분포에 가까워지는 것입니다.
\[x_T \approx \mathcal N(0,1)\]SDE와의 연결
위와 같이 정의한 정방향 확산 과정은 겉보기에는 단순히 이산적인 Markov chain으로 보입니다. 하지만 실제로는 연속 시간 확률 미분 방정식(Stochastic Differential Equation, SDE)을 작은 구간으로 쪼개어 Euler–Maruyama 방법으로 근사한 결과와 동일합니다. 예를 들어, VP-SDE(Variance Preserving SDE)는 다음과 같이 정의됩니다.
\[dX_t = -\tfrac{1}{2}\beta(t) X_t \,dt + \sqrt{\beta(t)}\, dW_t\]여기서 (dW_t)는 Wiener process(브라운 운동)이며, (\beta(t))는 시간에 따른 노이즈 주입률을 의미합니다. 이 식을 고정된 step 수 $T$로 나누고, Euler–Maruyama 방법으로 적분하면 다음과 같은 update 식을 얻을 수 있습니다.
\[X_{t+\Delta t} \approx \sqrt{1-\beta_t}\, X_t + \sqrt{\beta_t}\,\epsilon_t, \quad \epsilon_t \sim \mathcal{N}(0,I)\]이는 위에서 유도한 정방향 확산 과정 식과 정확히 일치합니다. 따라서 DDPM은 연속 시간 SDE를 이산화한 특수한 경우로 이해할 수 있습니다.
역방향 확산 과정
따라서 역방향 확산 과정은 가우시안 평균을 추정하는 문제로 변환됩니다. 아래 식에서 $\tilde{\beta_t}$ 계산에 사용되는 $\beta_t$들은 정방향 확산 과정의 전 구간 $t=1, \dots, T$에서 노이즈를 주입할 때 사용한 값들입니다. 이 값들의 배열을 $\beta$-schedule이라고 부릅니다.
\[p_\theta(x_{t-1} \vert x_t) = \mathcal{N}(\mu_\theta(x_t, t),\; \tilde{\beta_t}I)\] \[\tilde{\beta_t}=\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha}\beta_t, \qquad \bar{\alpha}_t = \prod_{s=1}^{t} (1 - \beta_s)\]가우시안 평균을 추정하는 문제에 대해 좀 더 자세히 살펴보겠습니다. (1)을 $x_{t-1}$에 대해 풀면 다음과 같습니다.
\[x_{t-1} = \frac{1}{\sqrt{1-\beta_t}} \Bigl(x_t-\sqrt{\beta_t}\varepsilon_t \Bigr)\tag{2}\]$\mu_\ast(x_t, t)$는 $x_{t-1}$의 기댓값이므로 다음과 같이 쓸 수 있습니다.
\[\mu_\ast(x_t, t)=\frac{1}{\sqrt{1-\beta_t}} \Bigl(x_t-\sqrt{\beta_t}\varepsilon_t \Bigr)\]그런데 여기에서 역방향 확산 모델이 가우시안 평균 $\mu_\ast(x_t, t)$를 추정할 수도 있지만, $\varepsilon_t$를 추정하는 문제로 바꾸면 계산이 편리해집니다. $\varepsilon_t$를 추정하는 역방향 확산 모델을 $\varepsilon_\theta(x_t, t)$라 하면 평균 추정치 $\mu_\theta$를 다음과 같이 쓸 수 있습니다.
\[\mu_\theta(x_t, t)=\frac{1}{\sqrt{1-\beta_t}} \Bigl(x_t-\sqrt{\beta_t}\varepsilon_\theta(x_t, t) \Bigr)\tag{3}\]$p_\theta(x_{t-1} \vert x_t)$는 모든 좌표축에서 동일한 분산을 갖는 다변량 가우시안 분포를 따르므로, negative log-likelihood를 구하면 아래와 같습니다.
\[-\log p_\theta(x_{t-1} \vert x_t) = \frac{\lVert \mathbf{x_{t-1}}-\mu_\theta(x_t, t) \rVert^{2}} {2\tilde{\beta_t}} + \text{const}\] \[-\log p_\theta \propto \lVert \mathbf{x_{t-1}}-\mu_\theta(x_t, t) \rVert^{2}\](2)와 (3)을 위 식에 대입하면, 상수배 $\beta_t/{1-\beta_t}$만 곱해질 뿐 구조는 동일하다는 것을 확인할 수 있습니다. 즉, 동일한 최적점을 갖습니다.
\[\lVert \mathbf{x_{t-1}}-\mu_\theta(x_t, t) \rVert^{2}=\frac{\beta_t}{1-\beta_t}\lVert \varepsilon_t-\varepsilon_\theta(x_t, t) \rVert^{2}\]결과적으로, DDPM에서 역방향 확산 과정에서는 노이즈 $\varepsilon$를 추정하게 됩니다.
1. 모델 학습과 이미지 생성
모델 학습
모델 학습 과정을 구체적으로 정리해보면 아래와 같습니다.
Step 1[정방향 확산 과정] timestep $t$를 뽑고, 원본 이미지 $x_0$에 $t$시점까지 정방향으로 노이즈를 누적해서 더한 이미지 $x_t$를 구합니다. 이전 포스트에서 설명한 닫힘 성질 덕분에 원본 이미지 $x_0$에 매 시점 노이즈를 누적해서 더하는 과정을 거치지 않고, $x_t$를 한 번에 샘플링할 수 있습니다. $\beta$-스케줄은 일반적으로 선형(1e-4 → 0.02) 또는 코사인 스케줄을 많이 사용합니다. $\beta$가 작을수록 이전 step의 정보가 많이 남기 때문에, 작은 $\beta$부터 시작해 서서히 노이즈를 키워야 역방향 학습이 안정적으로 이루어집니다.
Step 2[역방향 확산 과정] U-Net에 $x_t$와 시점 $t$를 입력해 $x_t$에 더해진 노이즈 $\varepsilon$를 예측합니다. 이 때, $t$는sinusoidal position embedding후에 MLP를 거친 다음ResidualBlock에FiLM방식으로 주입합니다. 아래 그림에서 실선 화살표가 UNet($p_\theta$)으로 노이즈를 추정하는 경로를 나타냅니다.
Step 3이미 알고 있는 정답 노이즈 $\varepsilon$와 U-Net을 통해 구한 노이즈의 예측값 $\hat\varepsilon_\theta$로 $\varepsilon$-MSE Loss를 계산하고 Adam optimizer로 파라미터를 업데이트합니다. 이전 포스트에서 설명한 바와 같이, $\varepsilon$-MSE Loss는 timestep별 $\sigma^2$ 가중 Denoising Score Matching(DSM) loss와 동치입니다. 따라서 둘 중 어떤 loss를 사용하든 같은 $\theta$에 수렴하게 됩니다. 다시 말해, $\varepsilon$-MSE를 최소화하면 스코어를 정확하게 예측할 수 있게 됩니다.
Step 3에서 설명한 스코어 함수는 다음과 같이 정의됩니다. 어떤 시점 $t$ (또는 노이즈 $\sigma_t$)에서의 확률 밀도 함수 $p_t(x_t)$가 주어졌을 때, 그 log-likelihood를 데이터 $x_t$에 대해 편미분한 벡터입니다. 이는 곧 log-likelihood를 빠르게 높이는 방향을 의미합니다.
이미지 생성 모델 관점에서 확률 밀도 함수 $p_t(x_t)$의 log-likelihood는 모델이 생성한 이미지 $x_t$가 얼마나 있을 법한 이미지인지를 나타낸다고 볼 수 있습니다. 스코어는 모델이 자연스러운 이미지를 만들어내기 위한, 노이즈 제거 방향입니다. 가우시안의 스코어 공식은 아래와 같습니다.
\[\nabla_{x}\,\log p(x) = -\frac{x-\mu}{\sigma^2}\]여기서 평균 $\mu=\sqrt{\bar{\alpha}_t}x_0$이고, 분산 $\sigma^2=1-\bar{\alpha_t}$이므로, $x_t$에 대한 스코어 함수는 다음과 같습니다.
\[\nabla_{x_t}\,\log p_t(x_t) = -\frac{x_t-\sqrt{\bar{\alpha}_t}x_0}{1-\bar{\alpha_t}}\]그리고 $x_t - \sqrt{\bar{\alpha}_t}x_0 = \sqrt{1-\bar{\alpha}_t}\varepsilon$이므로, 최종적으로 스코어 함수는 예측해야 할 노이즈 $\varepsilon$와 다음과 같은 관계를 갖습니다.
\[\nabla_{x_t}\,\log p_t(x_t) = -\frac{\sqrt{1-\bar{\alpha}_t}\varepsilon}{1-\bar{\alpha_t}}=-\frac{\varepsilon}{\sqrt{1-\bar{\alpha}_t}}\]이미지 생성(샘플링)
Step 1$x_T$를 초기화합니다. $x_T \sim \mathcal N(\mathbf 0,\mathbf I)$Step 2U-Net으로 $\varepsilon$를 예측하고, 이를 통해 스코어 함수를 간접적으로 추정합니다. U-Net이 잘 학습되면 $\hat\varepsilon_{\theta}(x_t,\,t) \approx \varepsilon$이므로, 다음과 같은 관계가 성립합니다.
Step 3Step 2에서 추정한 스코어 함수를 사용해서 매 역방향 step $x_t \rightarrow x_{t-1}$에서 $x_{t-1}$을 계산합니다. 이 과정에서 $x_t$가 스코어 방향으로 조금씩 수정되고, 그 누적 결과로 노이즈 $x_T$가 데이터 $x_0$로 복원됩니다.
2. 모델 구조
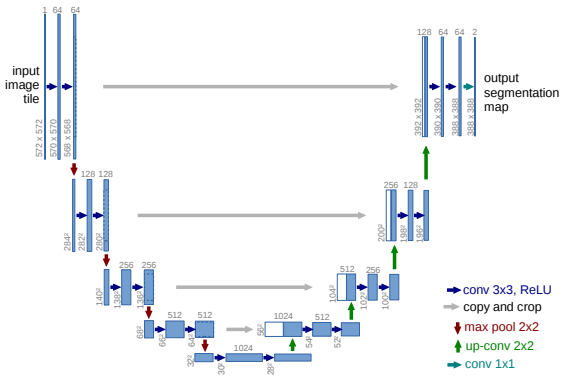
앞서 설명한 바와 같이 DDPM은 노이즈 $\varepsilon$를 예측할 때 U-Net을 사용합니다. DDPM에서는 기존 U-Net에서 Residual Block과 Multi-Head Attention을 추가해 사용했습니다. activation function으로는 SiLU(Swish)를 사용했습니다. 이곳에서 DDPM에 사용된 U-Net 코드를 확인할 수 있습니다.
Encoder (Contracting Path)
- Downsampling 및 feature 추출: 노이즈가 포함된 이미지 $x_t$와 sinusoidal position embedding을 거친 현재 timestep 정보 $t$를 입력받습니다. 여러 층의 Convolutional Layer와 Downsampling Layer를 통과하며 이미지의 공간적 해상도는 점진적으로 줄어들고, 대신 feature map의 채널 수는 증가합니다. 이 과정에서 이미지의 추상적인 feature가 추출됩니다.
Decoder (Expanding Path)
- Upsampling 및 이미지 재구성: Encoder의 마지막 단계에서 얻은 가장 압축된 feature map을 입력받아, Upsampling Layers와 Convolutional Layer를 통해 점진적으로 해상도를 늘려나갑니다. 이 과정에서 채널 수는 다시 줄어들며, 최종적으로 원본 이미지와 동일한 해상도의 노이즈 예측값 $\hat\varepsilon_\theta$을 출력합니다.
- Skip Connection: U-Net의 가장 중요한 특징 중 하나로, Encoder의 각 단계에서 Decoder의 상응하는 단계로 직접 연결되는 통로입니다. 위 U-Net architecture 그림에서 회색 화살표에 해당합니다. 이 Skip Connection은 Encoder에서 손실될 수 있는, 이미지 가장자리나 세부 질감같은 고해상도의 세밀한 공간 정보를 Decoder로 바로 전달합니다. Skip Connection 구조 덕분에 모든 스케일에서의 정보를 종합하여 노이즈 $\varepsilon$을 정확하게 예측할 수 있고, 결과적으로 고품질 이미지 복원을 가능해 집니다.
Residual Block
- Encoder와 Decoder의 각 단계에는 Residual Block이 포함됩니다. Residual Block은 입력에 여러 Convolutional Layer를 적용한 후 원본 입력을 더해주는 구조 $F(x)+x$로, 네트워크가 깊어져도 vanishing gradients 문제를 완화하고 정보 흐름을 개선하여 안정적인 학습을 돕습니다. 이는 DDPM이 복잡한 노이즈 패턴과 다양한 스케일의 이미지 feature를 학습하는 데 필수적입니다.
Multi-Head Attention
전역적 feature 포착: U-Net의 중간 해상도 단계에는 Multi-Head Attention이 사용됩니다. Convolutional Layer가 주로 지역적(local) feature를 포착하는 데 강한 반면, 이미지의 전체적인 구성 및 맥락, 객체들의 배치나 배경과 객체의 관계처럼 넓은 범위에 걸쳐 있는 전역적(global) feature를 포착하는 데는 한계가 있기 때문에 도입되었습니다.
- 이미지 품질 및 일관성 향상: Multi-Head Attention은 이미지의 다양한 영역 간의 복잡한 관계를 모델링하여, 생성되는 이미지의 일관성과 사실감을 높이는 데 기여합니다.
- 시간 정보 통합: timestep 정보 $t$를 나타내는 time embedding vector는 Multi-Head Attention block에도 입력됩니다. time embedding vector를 입력하는 대표적인 방식은 Query, Key, Value 각각에 time embedding vector를 더하거나 연결하는 것입니다. 이를 통해 모델이 각 노이즈 레벨에 맞는 적절한 전역적 feature를 학습할 수 있게 됩니다.
3. 한계
이전 포스트에서 설명했듯이, DDPM은 정방향 및 역방향 확산 과정을 이산적인 Markov Chain으로 정의했습니다. 이 때, $\beta_t$가 크면 이전 step의 정보를 거의 날려 버리고 큰 노이즈가 주입되므로, $x_t$가 $x_{t-1}$과 동떨어진 분포가 됩니다. 또한 U-Net이 한 번에 큰 노이즈 $\varepsilon$을 예측해야 합니다. 다시 말해, 모델이 풀어야 하는 문제의 난이도가 너무 높아지는 것인데요. 이런 경우 학습 안정성이 떨어지게 됩니다.
따라서 노이즈를 조금씩 주입해야 모델이 안정적으로 학습할 수 있으며, 샘플링 시에도 노이즈를 조금씩 제거해야 고품질의 이미지를 생성할 수 있습니다. 보통 샘플링에 필요한 총 step 수 $T$를 1000 내외로 설정해야 하는데요. 이는 곧 이미지 한 장을 만들 때마다 U-Net을 1000번 가량 호출해야 한다는 의미입니다. 이렇듯 DDPM은 샘플링에 너무 많은 시간이 소요되는 한계점이 있습니다.
DDPM 이후에 발표된 논문(Song et al., 2021)에서는 이산적인 Markov Chain을 연속 시간 관점으로 일반화했습니다. SDE를 고정된 step 수 $T$로 나누지 않고, 연속 시간 그대로 다루는 것입니다. 이렇게 하면 다양한 수치적분 기법을 자유롭게 사용할 수 있어서 step 수를 단축할 수 있습니다.
DDIM
DDPM의 역방향 확산 과정을 연속 시간 상미분 방정식(ODE)으로 해석하는 것도 가능한데, 이러한 방식을 제안한 논문이 DDIM입니다. 이 논문에서는 SDE에서 확률 항 $g(t)d\bar{w}_t$을 제거하여 매우 적은 step 수 만으로 확정적인 샘플링을 가능하게 만들었습니다.
\[dX_t = \Big[-\tfrac{1}{2}\beta(t) X_t - \beta(t)\,\nabla_{x_t}\log p_t(x_t)\Big] dt\]