[Paper Review] DDPM: Denoising Diffusion Probabilistic Models (1)
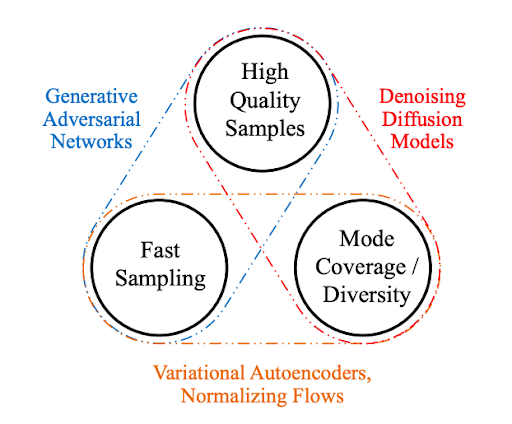
생성 모델은 데이터의 분포를 학습하여 그와 유사한 새로운 데이터를 생성하는 모델입니다. Vision 분야의 생성 모델로는 VAE와 GAN에 대해 다룬 바 있는데요. GAN은 고품질의 이미지를 생성할 수 있지만, adversarial learning 방식을 따르기 때문에 학습이 불안정한 편입니다. VAE는 GAN과 달리 likelihood 기반 생성 모델입니다. likelihood $p(x) = \int p(x \vert z)p(z)dz$는 현실적으로 계산하기 어려워서 variational inference를 사용해 이를 근사하는 ELBO를 최대화합니다. 아래 식에서 $p(x \vert z)$는 decoder가 학습하는 분포이고, 근사 사후 분포 $q(z \vert x)$는 encoder가 학습하는 분포입니다.
\[\log p(x) \ge \mathbb{E}_{q(z \mid x)} [\log p(x \mid z)] − D_{KL}(q(z \mid x) \mid\mid p(z))\]Normalizing Flows는 VAE와 같은 likelihood 기반 생성 모델로, 정규 분포같은 단순한 분포로부터 복잡한 데이터 분포로의 변환을 학습해서 이미지를 생성합니다. 역변환 가능한 구조 덕분에 정확하게 likelihood를 계산할 수 있습니다.
likelihood를 추론하는 VAE나 likelihood를 정확하게 계산해내는 Normalizing Flows 같은 likelihood 기반 생성 모델은 GAN보다 학습이 안정적이라는 장점이 있습니다. 또한 모델이 얼마나 자연스러운 이미지를 생성했는지 정량적으로 평가할 수 있습니다. GAN은 샘플링만을 위한 방법론이기 때문에 어느 정도로 그럴듯한 이미지를 생성했는지 확률로 표현할 수 없습니다. 하지만 GAN보다 상대적으로 흐릿한 이미지를 생성할 가능성이 높습니다.
이번 포스트에서 소개할 Denoising Diffusion Probabilistic Models (DDPM)은 diffusion process에 기반한 이미지 생성 모델입니다. DDPM의 핵심 아이디어는 timestep $t$에 따라 데이터에 노이즈를 점진적으로 확산(diffusion)시킨 다음, 그 과정을 거꾸로 학습하는 것입니다. likelihood 기반 최적화를 통해 학습 안정성을 높이면서도 고품질의 이미지를 생성할 수 있습니다. 이번 포스트에서는 DDPM을 이해하기 위한 Markov Chain과 Score Matching에 대해서 중점적으로 알아보고, 다음 포스트에서 DDPM에 대해 좀 더 자세히 알아보도록 하겠습니다.
1. Markov Chain
Markov Property를 만족하는 시퀀스를 Markov Chain이라고 합니다. Markov Property는 과거와 현재 상태가 주어졌을 때, 미래 상태 $X_t$의 조건부 확률 분포가 과거 상태들로부터 독립적으로 현재 상태 $X_{t-1}$에 의해서만 결정된다는 것을 뜻합니다.
\[\Pr\!\bigl(X_t = x_t \,\big|\, X_0 = x_0,\dots,X_{t-1} = x_{t-1}\bigr) \;=\; \Pr\!\bigl(X_t = x_t \,\big|\, X_{t-1} = x_{t-1}\bigr) ,\quad\forall\,t\ge 1.\]뒤에서 자세히 설명할 예정이지만, DDPM은 원본 이미지 $x_0$에 노이즈를 순차적으로 누적해서 더합니다. $x_{t-1}$에 노이즈를 더해 $x_t$를 만드는 과정을 반복하는 것입니다. 따라서 시퀀스 $x_0,…, x_T$는 Markov Chain이 됩니다.
\[x_t=\sqrt{1-\beta_t}\,x_{t-1}+\sqrt{\beta_t}\,\varepsilon,\;\varepsilon \sim \mathcal N(\mathbf 0,\mathbf I).\]노이즈로는 가우시안 노이즈가 사용됩니다. 저자들이 가우시안 노이즈를 선택한 이유는 계산 편의성 때문입니다. 조건부 관점에서 $x_{t-1}$는 상수 취급되고, $\varepsilon$는 표준 가우시안 벡터입니다. 가우시안은 선형 변환 후에도 가우시안이므로, $\varepsilon \sim \mathcal N(\mathbf 0,\mathbf I)$에 $\sqrt{\beta_t}$를 곱해도 가우시안이 유지됩니다. 따라서 조건부 분포 $q(x_t \mid x_{t-1})$도 평균이 $\sqrt{1-\beta_t}\,x_{t-1}$이고, 공분산이 $\beta_t \mathbf I$인 가우시안 분포를 따르게 되는 것입니다. 이러한 성질을 닫힘 성질이라고 합니다.
\[q\!\bigl(x_t \vert x_{t-1}\bigr) = \mathcal N\!\Bigl(\sqrt{1-\beta_t}\,x_{t-1},\;\beta_t \mathbf I \Bigr)\]2. Score Matching
Energy-Based Model (EBM)
에너지 기반 모델(Energy-Based Models, EBMs)은 데이터의 확률을 해당 데이터에 할당된 에너지를 통해 정의하는 모델입니다. 에너지가 낮은 데이터는 나타날 확률이 높고, 반대로 에너지가 높은 데이터는 나타날 확률이 낮다고 보는 것입니다. 이를 수식으로 표현하면 다음과 같습니다.
\[p_\theta(x)=\frac{\exp(-E_\theta(x))}{Z_\theta}\]- $x$: 이미지, 텍스트같은 데이터에 해당합니다.
- $E_\theta(x)$: 주어진 데이터 $x$에 대한 에너지 값을 출력하는 함수입니다. 이 함수는 보통 딥러닝 모델로 구현됩니다.
- $\exp(-E_\theta(x))$: 비정규화된 확률로, 에너지가 낮을 수록 이 값은 커지고 에너지가 높을 수록 이 값은 작아집니다.
- $Z_\theta$: 모든 가능한 데이터 $x$에 대한 $\exp(-E_\theta(x))$ 값의 합 또는 적분입니다. 즉, 전체 확률이 1이 되도록 만들어주는 정규화 상수입니다.
새로운 데이터를 생성할 때는 학습된 에너지 함수 $E_\theta(x)$에 따라 에너지가 낮은 영역에서 $x$를 샘플링합니다. 에너지 기반 모델을 다른 생성 모델들과 비교해보면 아래와 같습니다. GAN이 implicit density model인 데 반해, EBM, Normalizing Flow, VAE는 Explicit Density Model입니다. Explicit Density Model은 실제 데이터 분포 $p_\text{data}(x)$를 모델링하는 $p_\theta(x)$를 명시적으로 정의하고, 학습 데이터의 log-likelihood를 최대화하는 것을 목표로 합니다. Explicit Density Model 안에서도 EBM은 Normalizing Flow나 VAE 처럼 latent variable $z$를 상정하지 않고, 데이터 공간 자체에서 $p_\theta(x)$를 직접적으로 정의한다는 특징이 있습니다.
| 모델 | $p_\theta(x)$ | 주요 학습 방법 및 우회 전략 | 핵심 아이디어 |
|---|---|---|---|
| EBM | $p_\theta(x)=\frac{\exp(-E_\theta(x))}{Z_\theta}$ | MLE → Score Matching | 에너지 함수로 $p_\theta(x)$ 정의 |
| Normalizing Flow | $p_\theta(x) = p_z(f_\theta^{-1}(x)) \left| \det \left( \frac{\partial f_\theta^{-1}(x)}{\partial x} \right) \right|$ | MLE | 단순한 분포를 가역적 변환으로 복잡한 분포로 변환 |
| VAE | $p_\theta(x)= \int p_\theta(x \vert z)p_\theta(z)dz$ | MLE → ELBO 최대화 | Autoencoder의 Encoder과 Decoder를 확률 분포로 모델링 |
| GAN | - | adversarial learning | Adversarial learning을 통해 실제 데이터와 유사한 샘플 생성 |
EBM MLE의 현실적인 어려움
여타의 Explicit Density Model들처럼 EBM의 목적은 $p_\theta(x)$을 최대화하는 것이고, 이를 위해 이론적으로는 MLE를 사용합니다. MLE는 모델 $p_\theta(x)$가 학습 데이터셋을 가장 잘 설명하도록 하는 파라미터 $\theta$를 찾는 것입니다. 이는 데이터셋의 log-likelihood를 최대화하는 것과 같습니다.
\[\log p_{\theta}(x) = \log{(\frac{\exp(-E_\theta(x))}{Z_\theta})} = -E_\theta(x) - \log{Z_\theta}\] \[\theta^* = \arg \max_\theta \sum_{i=1}^{N} \log p_\theta(x_i)\]위 식을 파라미터 $\theta$에 대해 미분하여 gradient를 구합니다. 이 gradient는 파라미터 $\theta$를 업데이트 하여 log-likelihood를 최대화하는 데 사용됩니다.
\[\nabla_\theta \log p_\theta(x) = \nabla_\theta(-E_\theta(x)) - \nabla_\theta(\log Z_\theta)\] \[\nabla_\theta(\log Z_\theta) = E_{x \sim p_\theta(x)} [\nabla_\theta E_\theta(x)]\]여기에서 $\nabla_\theta(\log Z_\theta)$는 $p_\theta(x)$로부터 샘플링한 가짜 데이터 $x$의 에너지를 높이는 방향으로 파라미터 $\theta$를 업데이트 하는 부분입니다. 그런데 아주 복잡한 고차원 분포인 $p_\theta(x)$에서 의미있는 샘플 $x$를 얻는 것은 현실적으로 어렵습니다. $p_\theta(x)$에서 관찰 가능한 데이터 $x$가 무수히 많은데, 이 중에서 $p_\theta(x)$를 제대로 대표할 수 있는 샘플을 뽑아야 하기 때문입니다. $p_\theta(x)$를 제대로 대표하지 못하는 $x$가 샘플링되면 학습이 불안정해지므로 충분히 다양한 공간을 탐색해서 의미있는 샘플을 얻어야 하는데, 이 경우 샘플링에 너무 많은 시간이 걸립니다.
이처럼 정규화 상수 $Z_\theta$를 계산하는 것이 현실적으로 불가능하기 때문에 사용하는 방법이 바로 Score matching입니다. Score matching은 실제 분포 $p_\text{data}(x)$와 모델 $p_\theta(x)$의 스코어 함수를 최대한 가깝게 만드는 것을 목표로 하는 학습 방법입니다. 이에 따라 두 스코어 함수 사이의 차이를 최소화하는 아래와 같은 loss function을 사용합니다. 여기에서 스코어 함수는 log-likelihood의 $\theta$에 대한 gradient가 아니라 $x$에 대한 gradient로, $s(x)=\nabla_x \log p_\theta(x)$입니다.
\[L(\theta) = E_{x \sim p_{data}} \left[ \left\| \nabla_x \log p_{data}(x) - \nabla_x \log p_\theta(x) \right\|^2 \right]\]Score matching 방법을 사용하면 loss function을 미분하는 과정에서 정규화 상수가 상쇄되어 사라지기 때문에 정규화 상수를 계산할 필요 없이 모델을 학습할 수 있습니다.
DDPM과 Score matching의 관계
DDPM은 크게 정방향 확산 단계와 역방향 확산 단계로 이루어져 있습니다. 먼저 정방향 확산 단계에서는 원본 이미지에 여러 단계에 걸쳐 노이즈를 조금씩 더해 갑니다. 그 다음, 역방향 확산 단계에는 노이즈가 추가된 이미지를 입력받아서 이미지에 섞인 노이즈가 무엇인지 예측합니다.
DDPM의 역방향 확산 단계에서 이미지에 섞인 노이즈 $\varepsilon$를 예측할 때, loss function $\varepsilon$-MSE를 사용합니다.
\[\mathcal L_{\text{DDPM}} = \mathbb E_{t,\,x_0,\,\varepsilon} \bigl[ \,\bigl\|\, \varepsilon - \hat\varepsilon_{\theta}(x_t,\,t) \bigr\|_2^2 \bigr]\]그런데 $\varepsilon$-MSE를 최소화하는 것은 Denoising Score Matching의 loss function을 최소화하는 것과 사실상 동일함이 증명되었습니다. 이를 간단히 정리해보면 아래와 같습니다.
$x_t$는 $x_0$에 $\sqrt{1-\bar{\alpha}_t}$만큼의 스케일로 노이즈 $\varepsilon$가 더해진 형태입니다.
\[x_t=\sqrt{\bar{\alpha}_t}x_0 + \sqrt{1-\bar{\alpha}_t}\varepsilon, \qquad \varepsilon \sim \mathcal N(\mathbf 0,\mathbf I),\;\bar{\alpha}_t = \prod_{s=1}^{t} (1 - \beta_s)\]이 때, $x_t$에 대한 실제 분포의 스코어 함수 $\nabla_{x_t} \log p_t(x_t)$는 실제 노이즈 $\varepsilon$와 다음과 같은 관계를 가집니다.
\[\nabla_{x_t}\,\log p_t(x_t)=-\frac{\varepsilon}{\sqrt{1-\bar{\alpha_t}}}\]따라서 모델이 $\varepsilon$를 정확히 예측하도록 학습되면, 이는 곧 다음을 의미합니다.
\[-\frac{\hat{\varepsilon_\theta}(x_t, t)}{\sqrt{1-\bar{\alpha_t}}} \approx - \frac{\varepsilon}{\sqrt{1-\bar{\alpha_t}}}=\nabla_{x_t}\,\log p_t(x_t)\]노이즈 예측 모델 $\hat{\varepsilon_\theta}(x_t, t)$이 실제 노이즈 $\varepsilon$를 잘 맞추면, 그 모델은 간접적으로 실제 분포의 스코어 함수를 정확하게 추정하게 되는 것입니다.
3. DDPM
앞서 설명한 것처럼, DDPM의 정방향 단계에서는 원본 이미지에 노이즈를 점진적으로 더해 갑니다. 이렇게 하면 처음엔 이미지가 거의 그대로 이고, 단계가 지날수록 조금씩 흐려지다가 결국 완전히 랜덤한 노이즈로 변합니다. 왜 한 번에 노이즈를 더하지 않고, 단계별로 더하는 걸까요? 아래 이미지처럼 한 번에 심한 노이즈를 넣어버리면 원본 이미지와의 연결고리가 끊겨서 무엇을 복원해야 하는지 알기 어렵습니다.
하지만 아래와 같이 단계 별로 아주 작은 노이즈를 더하면 각 단계의 이미지는 Markov Chain의 특성을 띠게 됩니다. 이전 상태에만 의존하여 노이즈가 점진적으로 더해지므로, 원본 이미지의 핵심적인 특징들이 마지막 단계까지 유지되어 다음 단계에서 이를 근거로 노이즈를 정확하게 제거할 수 있습니다.
다시 말해, 복잡한 분포를 한 번에 맞추는 대신 덜 복잡한 분포를 반복적으로 맞추는 것입니다. 이렇게 하면 학습이 훨씬 안정적이고, 이미지의 품질도 좋아집니다. 다음 포스트에서는 DDPM 모델을 학습해서 이미지를 생성하는 과정을 수식과 함께 좀 더 자세히 살펴보겠습니다.