[Paper Review] DALL-E: Zero-Shot Text-to-Image Generation

DALL-E는 텍스트 설명만으로 이미지를 생성하는 text-to-image 모델입니다. 별도의 추가 훈련없이, 본 적 없는 조합의 텍스트에 대해서도 이미지를 생성할 수 있도록 학습되었다는 점이 중요한 특징입니다.

1. 모델 구조

DALL-E는 텍스트와 이미지 토큰을 하나의 데이터로 만들고, Transformer가 이를 입력받아 순서대로 예측하도록 학습합니다. 이 때, 이미지 픽셀 하나하나를 토큰으로 사용하면 자주 등장하는 디테일을 포착하는데 집중하게 됩니다. 우리가 물체를 시각적으로 인지할 수 있게 해주는 전체적인 구조에 대한 정보는 놓치게 되는 것입니다. 이러한 이유로, 저자들은 이미지를 양자화해서 Transformer의 입력값으로 사용했습니다. 구체적인 과정은 다음과 같습니다.

Stage 1. Train dVAE

VQ-VAE architecture

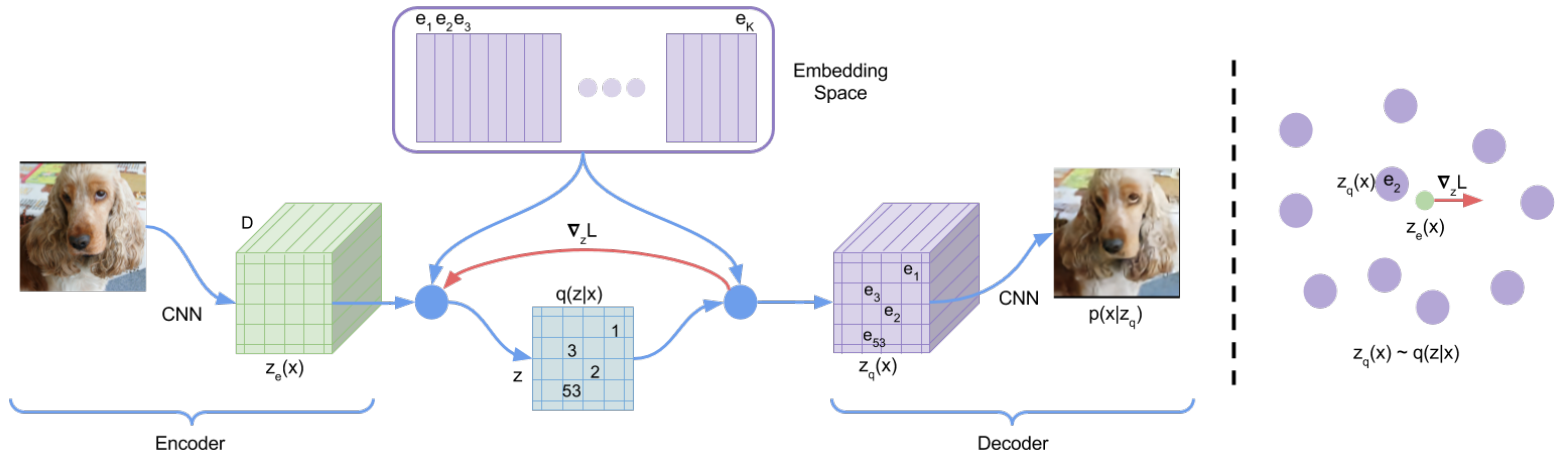
이미지 양자화는 VQ-VAE와 VQ-VAE-2에 대해 다룬 지난 포스트에서도 설명한 바 있는데요. DALL-E에서는 입력 이미지를 discrete 토큰으로 압축하기 위해 양자화 개념을 사용했습니다. discrete variational autoencoder (dVAE) 모델을 학습시켜 256 X 256 크기의 RGB 이미지를 32 X 32 크기의 discrete 토큰으로 만들었습니다. 이미지를 토큰화할 때 사용한 codebook의 크기는 8192입니다.

Encoder는 7 X 7 kernel로 시작해서, 주로 3 X 3 kernel로 구성된 ResNet 구조입니다. 마지막 kernel 크기는 1 X 1로, 32 x 32 x 8192 크기의 feature map을 만듭니다. codebook에 포함된 8192개 index 각각에 대한 logit을 출력하는 것입니다.

Stage 2. Train Transformer

Stage 1에서 만든 32 X 32 크기의 이미지 토큰을 BPE로 encoding한 최대 256 크기의 텍스트 토큰에 뒤이어 붙여서 Transformer의 입력 값으로 사용합니다. Transformer decoder만 사용해서 과거 토큰들로 다음 토큰을 예측했는데요. 현재 토큰을 예측할 때 미래 토큰은 볼 수 없으므로, 이러한 모델은 autoressive 모델이라고도 부릅니다. 아래 수식에서 $x_1$부터 $x_{N}$까지가 텍스트 토큰, $x_{N+1}$부터 $x_{N+M}$까지가 이미지 토큰입니다.

\[P(x_1, x_2, \ldots, x_{N+M}) = \prod_{t=1}^{N+M} P(x_t \mid x_1, x_2, \ldots, x_{t-1})\]

Transformer 구조를 좀 더 자세히 살펴보면, 64개의 attention layer로 이루어져 있고, 각각의 attention layer는 62개의 attention head를 가지고 있습니다. $x_1$부터 $x_{N}$까지 적용되는 text-to-text attention은 일반적인 causal mask를 사용하고, $x_{N+1}$부터 적용되는 image-to-image attention은 세 종류의 sparse mask를 사용했습니다. 아래 네 개 mask의 왼쪽 부분은 모두 마스킹 되어 있지 않은데, 이 부분이 텍스트 토큰에 해당합니다. 이미지 토큰을 생성할 때는 모든 텍스트 토큰을 볼 수 있는 것입니다. 마지막 64번째 self-attention layer에만 convolutional attention mask(d)를 사용하고, 나머지 layer에서는 row attetion mask(a)와 column attention mask(c)를 섞어서 사용했습니다. (c)는 GPU 효율을 높이기 위해 (b)를 변형한 버전입니다.

2. 모델 학습

모델이 학습되는 전체 과정은 evidence lower bound (ELB)를 최대화하는 과정입니다.

\[\ln p_{\theta, \psi}(x, y) \ge \mathbb{E}_{z \sim q_\phi(z|x)} \left[\ln p_\theta(x | y, z) \right] - \beta \, D_{\mathrm{KL}} \bigl(q_\phi(z \mid x) \; \| \; p_\psi(y, z) \bigr)\]

위 수식에서 $x$는 RGB 이미지, $y$는 텍스트, $z$는 이미지의 discrete 토큰으로 이루어진 sequence입니다. 그리고 $q_\phi(z \mid x)$는 dVAE Encoder가 이미지 $x$로부터 얻은 32 x 32 discrete 토큰의 분포, $p_\theta(x \mid y, z)$는 dVAE Decoder가 $y$와 $z$로부터 RGB 이미지를 생성하는 분포입니다. $p_\psi(y, z)$는 Transformer가 모델링하는 부분으로, 텍스트 토큰 $y$와 이미지 토큰 $z$의 결합 분포입니다. Stage 1에서는 초기 $p_\psi$를 uniform categorical distribution으로 고정하고, $\phi$와 $\theta$에 대해 ELB를 최대화합니다. Stage 2에서는 $\phi$와 $\theta$를 고정하고, $\psi$에 대해 ELB를 최대화합니다. 이제 각각의 term을 자세히 살펴보겠습니다.

• $ \ln p_{\theta, \psi}(x, y) $ 이미지 $x$와 텍스트 $y$를 생성할 확률의 로그 값이고, 이를 최대화하는 것이 최종 목표입니다.
• $ \mathbb{E}_{z \sim q_{\phi}(z | x)}\left[ \ln p_\theta(x | y, z) \right] $ dVAE가 $y$와 $z$로부터 원본 이미지 $x$를 얼마나 잘 복원하는지를 나타냅니다.
• $ \beta \, D_{\mathrm{KL}} \bigl(q_\phi(z \mid x) \; | \; p_\psi(y, z) \bigr) $ KL divergence term으로, 실제 이미지 $x$로부터 추정한 discrete latent 분포 $q_\phi(z \mid x)$와 Transformer가 학습한 분포 $p_\psi(y, z)$ 사이의 차이를 측정한 것입니다. $\beta$는 KL divergence의 가중치입니다.

학습 데이터

• 2억 5천만 개 이상의 이미지-텍스트 쌍 수집
• Conceptual Captions, Wikipedia, YFCC100M 데이터셋 사용
• 텍스트가 너무 짧거나 영어가 아니면 제외
• 텍스트가 “photographed on <date>” 처럼 상투적인 문구인 경우도 제외
• 가로세로 비율이 [1/2, 2] 범위 밖에 있는 이미지 제외 (너무 길거나 좁은 이미지 제외)

3. 모델 성능

위 이미지들은 DALL-E로 생성한 것입니다. 동물과 아코디언이라는 서로 다른 개념을 자연스러운 형태로 결합하거나, 동물을 의인화 하거나, 텍스트를 그리는 등의 지시를 잘 수행한 것을 확인할 수 있습니다.